I’ve watched a lot of NBA basketball in my day, and one of the things I find most fascinating is to look back on specific moments that have far-reaching implications for individual players, teams, and the narratives that make the League so compelling. There are a few moments that fans resurface often- Michael Jordan deciding to retire (for the 2nd time) in 1998, Ray Allen making a crucial game-tying shot in the 2013 Finals, JR Smith’s lapse of judgment in the 2018 Finals, and more.
There is another moment that doesn’t get mentioned as often, but the more I reflect on it, the more I find it absolutely mind-boggling: the Houston Rockets missing 27 consecutive (!!) three-pointers en route to losing Game 7 of the 2018 Western Conference Finals. 27 missed threes in a row! When I first heard that number I thought that it had to be a record, which I recall being confirmed on the TV broadcast. Without this record-setting meltdown, the Rockets might have won that game and made it to the Finals– which would have had huge implications for many important players– so I wanted to deep dive into the data for missed three-pointers and discuss some of the potential implications of that game.
The Background
Let’s quickly review the scenario for the game in question. The Houston Rockets matched up with the Golden State Warriors in the 2018 Western Conference Finals, competing for the chance to go to the NBA Finals and play for the championship.
The Warriors had won the championship the year before in 2017, their 2nd in just 3 years. They were seen as the prohibitive favorite to win the 2018 championship, since they had former NBA MVP Kevin Durant alongside two-time MVP winner Steph Curry and a strong supporting cast. Many saw the level of talent on their team to be overwhelming, and most NBA fans assumed the Finals matchup would once again be Steph Curry’s Warriors facing off against LeBron James’ Cavaliers- the exact same matchup the NBA had had for three consecutive years from 2015-2017.
The Rockets gave the Warriors a run for their money, jumping out to a 3-2 series lead going into Game 6, now just one win away from punching their ticket to the Finals. Unfortunately, they would have to close out the series without one of their best players, Chris Paul, who went down with an injury in Game 5. The Warriors would win Game 6 in a blowout, setting up an all-or-nothing, series-deciding Game 7. Could the Rockets figure out a way to do the impossible- win Game 7 on the road to eliminate the Warriors juggernaut and shock the world in the process?
The short answer is: no, they couldn’t. The Warriors won the game 101-92, with the Rockets aforementioned abysmal shooting night being a big part of the reason why. The Rockets went just 7/44 (15.91%) from three that game, far below their 36.2% average on the season. Let’s see if we can put into perspective using NBA data how rare it is to shoot as poorly as they did that night.
Getting the Data
There are a few angles I want to look at to help put this Rockets game into perspective:
- We already know that 27 consecutive three point misses in a single game set the record- how often do teams even come close to that number?
- Are there any streaks of consecutive missed three pointers spanning multiple games that eclipse the Rockets’ 27?
- If we look at the total number of threes the Rockets missed that game, how does that compare to other poor shooting nights in NBA history?
- Since I already have the data, what are the results above if we analyze three points streaks by player instead of by team?
To get started, I had to identify where we can get the data we need, including play-by-play data so we can extract missed three-point streaks. Fortunately, the Python nba_api package created by swar (https://github.com/swar/nba_api) can be utilized for this exact purpose.
The nba_api package contains a couple of relevant endpoints:
- The LeagueGameLog endpoint, which can be queried to retrieve high level game data
- The PlayByPlayV2 endpoint, which we can query one game a time to retrieve play-by-play data from 1997/98 season up to 2022/23
Included in my repository are get_game_logs.py (for accessing the game logs) and get_pbp.py (for accessing and formatting the play-by-play data for each game from the game logs). Since each game’s play-by-play data has to be retrieved one at a time, it takes about 7 hours to complete. The relevant results from each are stored in a local SQLite database.
Extracting Streaks From Play-by-Play Data
Once I stored the data I needed in a local database, the next step was to extract the streaks (consecutive made or missed three pointers). Below are the steps I took.
#1 Load play-by-play data
I loaded the play-by-play data from my local SQLite database using a Python script, while sorting the data by the Team ID, Game Date, and Event Number. I filter the rows where the Description contained the string “3PT” so I only got three point shots.
SELECT pbp2.GAME_ID, lgl.GAME_DATE, EVENTNUM, pbp2.HOMEDESCRIPTION, pbp2.VISITORDESCRIPTION,
PLAYER1_ID, PLAYER1_NAME, PLAYER1_TEAM_NICKNAME, PLAYER1_TEAM_ID ,
CASE
WHEN COALESCE(HOMEDESCRIPTION, '') <> '' THEN HOMEDESCRIPTION
ELSE VISITORDESCRIPTION
END AS DESCRIPTION
FROM PLAY_BY_PLAYS_STATS_2 pbp2
LEFT JOIN LEAGUE_GAME_LOGS lgl ON pbp2.GAME_ID = lgl.GAME_ID
WHERE lgl.WL = "W" AND DESCRIPTION LIKE "%3PT%
ORDER BY pbp2.PLAYER1_TEAM_ID, GAME_DATE, pbp2.GAME_ID, EVENTNUM
"#2 Identifying 3 Point Streaks
I iterated through each row to determine whether the shot was a make or a miss. If the shot result is the same as the shot in the previous row, and is from the same game, I added one “point” to the a streak counter (game_streak_val) for a make or subtracted one for a miss. That way the missed shot streaks will be negative number values.
The streaks are identified by their streak_id and game_id– that way I can later find the number of misses or makes in a streak from a single game, or add streaks together if they have a different game_id but the same streak_id.
Here’s a snippet of the logic for determining the game streak value for each shot:
def get_new_streak_val(prev_val, is_make, should_reset_streak_val):
#If the shot is make, add one; if miss subtract
streak_point = int(is_make) or -1
added = prev_val + streak_point
if should_reset_streak_val or abs(added) < abs(prev_val):
new_val = streak_point
else:
new_val = added
return new_valNow I have a Pandas Dataframe representing each 3 point shot in the database and assigns a streak_id, and lists its position within the streak (game_streak_val).
Here’s a sample of the data at this step:
| game_id | event_num | team_id | player_id | streak_id | game_streak_val |
|---|---|---|---|---|---|
| 0029600005 | 415 | 1610612737.0 | 80 | 6 | -1 |
| 0029600005 | 427 | 1610612737.0 | 302 | 6 | -2 |
| 0029600017 | 20 | 1610612737.0 | 302 | 6 | -1 |
| 0029600017 | 36 | 1610612737.0 | 363 | 6 | -2 |
| 0029600017 | 61 | 1610612737.0 | 120 | 7 | 1 |
| 0029600017 | 91 | 1610612737.0 | 302 | 8 | -1 |
#3 Aggregating the results
Right now each shot from each game streak is represented in the data. The data needs to be aggregated so the max value of each game streak is represented. In the following snippet I convert the negative values to positive, find the MAX of each streak (by game_id and streak_id), and then convert the values back to negative.
def agg_streaks_by_game(df, streak_criteria):
cols= {
"player_id":["player_id", "player_name"],
"team_id": ["team_id" , "team_name"]
}
game_streaks_df = df.copy()
game_streaks_df["is_make"] = np.where(game_streaks_df["game_streak_val"] > 0, True, False)
game_streaks_df["game_streak_val"] = game_streaks_df["game_streak_val"].abs()
game_streaks_df = game_streaks_df.groupby(["streak_id","game_id", "is_make"] + cols[streak_criteria], as_index=False)["game_streak_val"].max()
game_streaks_df["game_streak_val"] = np.where(game_streaks_df["is_make"] == False, game_streaks_df["game_streak_val"] *-1, game_streaks_df["game_streak_val"])
print("games_df")
print(game_streaks_df)
return game_streaks_dfNow, the results of the above are aggregated so that we are able to 1) count the number of games that feature a shooting streak for each streak value, and 2) join those results with an aggregation that counts the number of streaks where the total of the game_streak_val at the streak_id level matches each streak value.
def agg_streak_counts(df):
# Aggregate counts
game_count_df = df.groupby('game_streak_val')['game_id'].count().reset_index(name='game_count')
streak_count_df = df.groupby('streak_id')['game_streak_val'].sum().value_counts().reset_index(name="streak_count").sort_index()
merged = streak_count_df.merge(game_count_df, on="game_streak_val", how="outer")
# Rename columns
merged = merged.rename(columns={'game_streak_val': 'streak_val'})
#merged = merged["streak_val", "game_count", "streak_count"]
merged["game_count"] = merged['game_count'].fillna(0)
merged["game_count"] = merged["game_count"].astype('int')
merged = merged.sort_values(by="streak_val")
merged = merged.reset_index(drop=True)
print("merged df")
print(merged)
return mergedPlease take a look at the GitHub repository for the code for all Python scripts I used: https://github.com/richparks92/missed-threes.
Analyzing the Data
Now that I have the data formatted the way I want, I can answer the questions I asked around how rare a 27-consecutive three point miss shooting streak is, and put some context around the Rockets’ shooting night as a whole. To visualize the data, I created a data story using Tableau Desktop (Public Edition). You can see the story here: https://public.tableau.com/app/profile/chris.parks/viz/3PTStreaksStory/3PTStreaksStory?publish=yes.
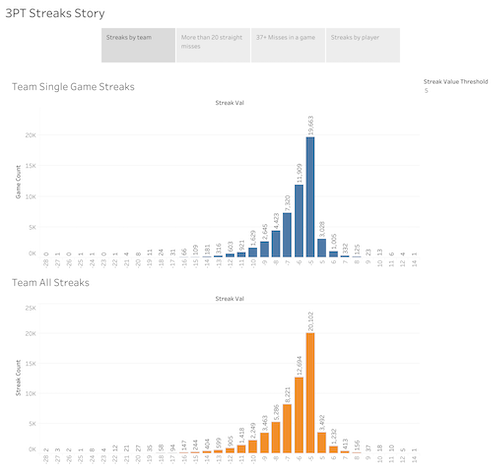
Let’s take a look at some of the findings. The first tab, “Streaks by team” shows the number of single games where a team has hit or missed x number of consecutive shots (top) as well as a similar chart that takes streaks spanning multiple games into account (bottom). The screenshot only shows make or miss streaks of 5 or more consecutive shots to help keep perspective- if you open the Tableau link you can edit the “Streak Value Threshold” to see all of the streaks. As you can see, we can confirm that there’s only one occurrence where a team missed 27 straight threes in a game (the Rockets) and only four total games where a team missed 22 or more straight threes. In total there are over 330,000 missed three point streaks of at least one shot, so it’s incredibly rare. For streaks spanning multiple games, it’s a little less rare, as there are two occurrences where teams missed 28 straight and 20 occurrences where teams missed 22 or more.
The next tab lists the multi-game occurrences of missed three streaks over 20 in case you were curious which teams have done this and when. There’s also a simple bar graph showing the disparity between missed three point streaks over and under 20 shots.


Now that I’ve confirmed my suspicion about the rarity of missing 27 straight three pointers, I want to also see if the total number of missed threes is as rare. The Rockets missed 37 threes overall out of the 44 they took in the Game 7 loss to the Warriors, and looking at the data that number of misses is uncommon but is not as rare. Using a SQL query, I found that since the NBA instituted the three point line in 1979, only 83 times out of 106428 (0.08%) has a team missed 37 or more threes. However, teams have only shot 44 or more threes as the Rockets did that night 1513 times, just 1.42% of qualifying games, meaning it’s somewhat rare that a team takes that many threes in a single game across NBA history. Of those 1513 games where a team shot at least 44 threes, 80 of them resulted in 37 or more misses (5.29%). For more detail, you can look at the the table in the “37+ misses in a game” tab of the Tableau story, which shows the instances where teams missed at least 37 threes.
What about three point shooting streaks for players? We can gain some insight from the “Streaks by Player” tab. Here we see that the most threes made by a player in a row is 10 in a single game, and 13 across multiple games; each of these occurred three times. Eric Gordon and Brook Lopez have the most consecutive misses in a single game at 12 each, while Zaza Pachulia set the record for most consecutive misses across games with 33. Zaza went 0/33 in his career from three- since he was not a three point shooter, it’s safe to assume that most or all of these attempts were last-second heaves to beat the buzzer or the shot clock.

Conclusion
By looking through the available play-by-play and game log data, we see that missing around the number of threes in a row as the Rockets’ 27 straight is extremely rare. We also saw that they shot a relatively high number of threes, which made it more likely that they missed the total amount that they did, although even when accounting for the number of attempts the chances of missing at least 37 total is still unlikely.
I think about this game so much because as it was happening, it felt like an incredibly rare occurrence was the only thing preventing a historically shocking playoff upset, and I can’t help but wonder how things would have played out if that didn’t happen. The Rockets lost by 9 points, so making three more threes could have potentially tied the game; even if they only made one or two more to break up the missing streak, who knows what that could have done for the Rockets’ momentum and morale during the game?
The potential implications of the Rockets winning and advancing to the Finals, as I mentioned in the beginning of this post, could have been huge. Here are some of the implications I’ve considered:
- The Warriors team that beat the Rockets is considered one of the most (if not the most) talented NBA team to be assembled.
- If they lost the series, would people look at Steph Curry differently? He had already won two championships up until that point, so maybe people wouldn’t hold a playoff disappointment against him.
- Kevin Durant, also on that Warriors team, might have been looked at differently. Some fans argue now that he was only able to win championships because he joined an already stacked team that had won a championship before without him- losing this series would have only added fuel to the fire.
- Kevin Durant ended up leaving the Warriors after the 2018-2019 season, but would losing in the playoffs twice and only winning one championship with all the talent on the team cause him to actually stay if that had happened?
- I believe the careers of several Rockets would have been seen differently if they had made it to the Finals that year, even if they didn’t win the championship.
- James Harden, who also won the MVP award that season, was the team’s best player and was in his prime. Unfortunately for him, he’s had a few playoff series where he was not able to rise to the occasion and play his best ball, and many view this as a significant blemish on his otherwise stellar résumé. Beating such a talented team to advance to the Finals would have done wonders for his postseason reputation.
- Chris Paul was the Rockets’ second-best player that year, and missed the final two games of the series due to injury. Although many such as myself consider him to be one of the best point guards of all time, he has a postseason résumé similar to Harden’s, with some disappointing playoff exits. If he had not gotten hurt, could he have helped propel the Rockets to victory?
- Mike D’Antoni, the coach of the Rockets at the time, is in my opinion overlooked sometimes as an innovator of offensive strategy. D’Antoni has not yet made the Finals in his career. In 2022, the NBA released a list of who they consider the 15 best coaches in NBA history- could a Finals berth have solidified D’Antoni’s spot on this list?
- This game may have impacted the legacies of more than just the players and coaches in the series.
- If the Rockets had won Game 7 and went to the Finals, they would have met LeBron James and the Cleveland Cavaliers to compete for a championship. The Warriors ended up making it and winning the championship instead. Could LeBron have beaten the Rockets for his 4th title? How would that affect his legacy, and would that be enough to keep the Cavaliers together, whose roster was shaken up the following season?
As fun as it is to wonder all of these different scenarios, the answer for each of them is the exact same- we’ll never know.